C++ 两点之间最短距离

两点之间最短距离

这是我的一个测试，也是我学习html的/起点，他们说一个合格的程序员必须学会html，我比他们起步晚了一些，可是我认为还来的及，以后我就用html来记录我的学习记录了。

问题的提出： 在二维平面的n个点上，找出其中的一对点，使得在n个点组成的所有的点中，该点对的距离最小。

一维：最接近点对问题

方法一：（暴力法）   直接使用双层遍历来计算每一对点的距离，另外新建一个变量记录两点之间距离最小的值，但是如此一来时间复杂度就变为O(n²),

方法二：(分治法） 分治法的思路:

划分成子规模点集S1和S2； 找到S1和S2的最小距离d； 合并S1和S2：利用d在S1的(m-d,m]和S2(m,m+d]中找到最大点和最小点，即p3和q3.选出最小距离，完成合并。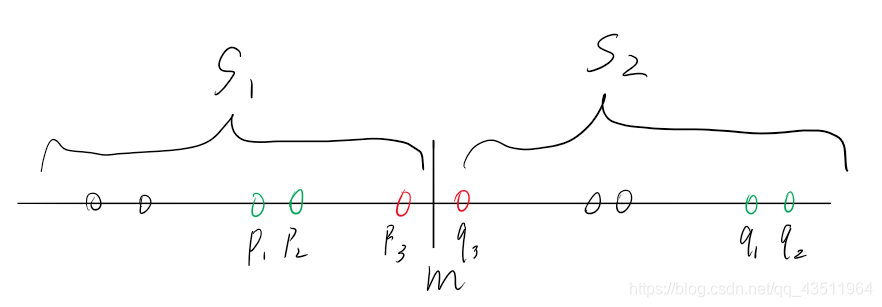 

m如何选择 m=(max(s)+min(s))/2;

代码： talking is cheap,show me the code; /*根据算法随便写的，返回的是两个点之间最小的距离，不是两个点的坐标，如果有问题，欢迎指正*/ /*这里的坐标默认为正序的*/ #include<iostream> #include<vector> using namespace std; int search(vector<int> target) { int n=target.size(); if(n<2) //如果分到一个元素就返回最大数值 return INT_MAX; int mid=n/2; //中线 vector<int> temp_left; vector<int> temp_right; temp_left.insert(temp_left.begin(),target.begin(),target.begin()+mid); //中线分割 temp_right.insert(temp_right.begin(),target.begin()+mid,target.end()); int p=search(temp_left); int q=search(temp_right); int d=temp_right.front()-temp_left.back(); cout<<temp_right.front()<<" "<<temp_left.back()<<endl; return d>min(p,q)?min(p,q):d;}//返回两边和贯穿中间的最小的两点距离 int main(){ int a[6]={-9,-6,0,4,7,9}; vector<int> target(a,a+6); cout<<search(target); return 0; } 二维最接近点的问题：

思路与一维的最接近点对相似。

选取中垂线l：x=m来作为分割直线。 递归的在S1和S2找出其最小距离d1和d2，并设d=min{d1,d2}，S中最接近点对或是d，或者是某个{p，q} 合并起来

// 随便写思路的如果有误，请指正（注意返回的是两点之间的距离，不是坐标） #include <iostream> #include <math.h> #include<algorithm> using namespace std; struct point { int x, y; }; double distance(struct point p1, struct point p2) { return sqrt(pow(p1.x - p2.x, 2) + pow(p1.y - p2.y,2)); } double search(struct point p[],int pl,int pr) { if (pl == pr) return INT_MAX; int mid = (pl + pr) / 2; double d_left = search(p, pl, mid); double d_right = search(p, mid + 1, pr); double temp_d = min(d_left, d_right); while (abs(p[pl].y - p[mid].y) > temp_d&&pl < pr)//如果仅仅是单边距离就已经大于上一次比较返回的d就没必要在接下来的敌方继续比较了。 pl++; while (abs(p[pr].y - p[mid].y) > temp_d&&pl < pr) pr--; for (int i = pl; i < pr; i++) { for (int j = i + 1; j < pr; j++) { if (temp_d < abs(p[i].x - p[j].x))//同理与上面的注释 break; else temp_d = min(temp_d, distance(p[i], p[j]));//找到最小的距离 } } return temp_d; } int main() { struct point p[100]; int n; cin >> n; for (int i = 0; i < n; i++) { cin >> p[i].x; cin >> p[i].y; } cout<<search(p, 0, n - 1); }